문제 설명

무인도에 갇힌 사람들을 구명보트를 이용하여 구출하려고 합니다. 구명보트는 작아서 한 번에 최대 2명씩 밖에 탈 수 없고, 무게 제한도 있습니다.
예를 들어, 사람들의 몸무게가 [70kg, 50kg, 80kg, 50kg]이고 구명보트의 무게 제한이 100kg이라면 2번째 사람과 4번째 사람은 같이 탈 수 있지만 1번째 사람과 3번째 사람의 무게의 합은 150kg이므로 구명보트의 무게 제한을 초과하여 같이 탈 수 없습니다.
구명보트를 최대한 적게 사용하여 모든 사람을 구출하려고 합니다.
사람들의 몸무게를 담은 배열 people과 구명보트의 무게 제한 limit가 매개변수로 주어질 때, 모든 사람을 구출하기 위해 필요한 구명보트 개수의 최솟값을 return 하도록 solution 함수를 작성해주세요.
제한사항
무인도에 갇힌 사람은 1명 이상 50,000명 이하입니다.
각 사람의 몸무게는 40kg 이상 240kg 이하입니다.
구명보트의 무게 제한은 40kg 이상 240kg 이하입니다.
구명보트의 무게 제한은 항상 사람들의 몸무게 중 최댓값보다 크게 주어지므로 사람들을 구출할 수 없는 경우는 없습니다.
입출력 예
| people | limit | return |
| [70,50, 80, 50] | 100 | 3 |
| [70, 80, 50] | 100 | 3 |
나의 풀이
def solution(triangle):
for i in range(1, len(triangle)):
for j in range(len(triangle[i])):
if j == 0:
triangle[i][j] += triangle[i-1][j]
elif j == len(triangle[i])-1:
triangle[i][j] += triangle[i-1][j-1]
else:
triangle[i][j] += max(triangle[i-1][j], triangle[i-1][j-1])
return max(triangle[-1])
2차원 배열임을 이용해 이중for문을 이용하여 이 문제를 풀었다.
먼저 위 문제에서의 삼각형을 확인해보자.
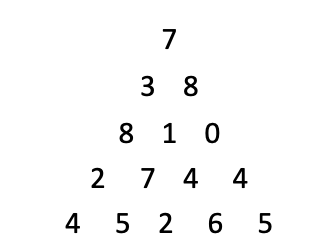
위 정수 삼각형에서 맨 위에 있는 꼭짓점인 7을 제외하면 삼각형에서 가장 밖에 있는 숫자는 동일한 변의 위에 있는 숫자와 더해질 수 밖에 없다.

이 초록색과 노란색으로 칠해진 부분을 처리하기 위해서 j == 0인 경우와 j == len(triangle[i])-1인 경우를 나누어서 처리했다.
이제 남은 부분은 색이 칠해지지 않은 수를 처리하는 것인데 이를 위해 위층에 있는 숫자 중 더 큰 숫자를 뽑아 더해주면 된다는 생각을 했다.

위 이미지에 있는 삼각형은 j == 0인 경우와 j == len(triangle[i])-1인 경우를 처리했을 때의 삼각형의 모습이다.
이제 색이 칠해지지 않은 수의 1과 그 윗 라인에 있는 10, 15를 비교하여 더 큰 수를 1과 더해주면 된다.
이 때 더 큰 수는 15이므로 값을 더한 삼각형에서 1의 자리는 16이 된다.

이와 같은 방식으로 18과 16을 비교하여 7과 더하고 16과 15를 비교하여 더 큰 수를 4와 더해주고
그 아래줄 역시 같은 논리로 더해주면 값을 더한 삼각형의 최종 모습은 아래의 이미지와 같을 것이다.

이 과정을 일반화 시키면 triangle[i][j] += max(triangle[i-1][j], triangle[i-1][j-1])로 작성할 수 있다.
이를 else문을 통하여 처리하였다.
그 후 정수 삼각형에서 가장 마지막 라인에 있는 숫자 중 가장 큰 수를 max를 이용해 리턴하였다.
또한 이 문제에 대한 기본적인 접근 방식은 동적 계획법(Dynamic Programming, DP)으로 DP에 대해 간략히 정리해보자.
동적 계획법(Dynamic Programming, DP)
복잡한 문제를 작은 부분으로 나누어 해결한 후 그 해결 방법을 저장하여 더 큰 문제를 해결할 때 이를 재사용하는 방법이다.
동적 계획법(Dynamic Programming, DP)의 주요 개념
1. 분할 정복
큰 문제를 작은 부분으로 나눈다.
2. 메모이제이션
한 번 계산한 부분 문제의 결과를 저장하고 필요할 때마다 꺼내어 사용한다.
동적 계획법(Dynamic Programming, DP)을 적용하기 위한 조건
1. 중복 부분 문제
큰 문제와 작은 문제를 같은 방법으로 해결할 수 있어야한다.
2. 최적 부분 구조
전체 문제의 최적해가 부분 문제의 최적해로 구성되어야한다.
'Coding Test' 카테고리의 다른 글
| [CT] Programmers 구명보트 JavaScript ver. (0) | 2023.08.14 |
|---|---|
| [CT] Programmers 구명보트 Python3 ver. (0) | 2023.08.14 |
| [CT] Programmers 문자열 정수의 합 Python3 ver. (0) | 2023.08.12 |
| [CT] Programmers 문자열 정수의 합 Javascript ver. (0) | 2023.08.12 |
| [CT] Programmers 영어 끝말잇기 Javascript ver. (0) | 2023.08.10 |



